Convex Optimization-culled from http://en.wikipedia.org/wiki/Convex_programming
Convex minimization, a subfield of optimization, studies the problem of minimizing convex functions(a function whose graph of real values is below the line segment joining two points of this graph) over convex sets. The property that makes an optimization convex can make it in some sense "easier" than the general case - for example, any local minimum must be a global minimum.
Given a
real
vector
space
 together with a convex, real-valued
function
together with a convex, real-valued
function
defined on a convex subset (i.e a set
of two points that lie in an object whose straight line segment has points on it
that also lie in the object)
 of
of
 .
As such the issue is to find any point
.
As such the issue is to find any point
 in
in
 for which the number
for which the number
 is smallest, i.e., a point
is smallest, i.e., a point
 such that
such that
-
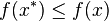 for all
for all
 .
.
Convex optimization case
An optimization case (also referred to as mathematical programming
program or minimization problem) of finding some
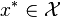 such that
such that
where
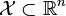 is the feasible set and
is the feasible set and
 is the objective, is called convex if
is the objective, is called convex if
 is a closed convex set and
is a closed convex set and
 is convex on
is convex on
 .
[1]
[2]
Alternatively, an optimization problem on the form
.
[1]
[2]
Alternatively, an optimization problem on the form
is called convex if the functions
 are convex.[3]
are convex.[3]
Theory
The following statements are true about the convex minimization problem:
- if a local minimum(a minimum within some neighbourhood that need not be a global one) exists, then it is a global minimum(the smallest value of a set, function, over its entire range).
- the set of all (global) minima is convex.
- for each strictly convex function, if the function has a minimum, then the minimum is unique.
Standard form
Standard form consists of the following three parts:
- A convex function
 to be minimized over the variable
to be minimized over the variable

- Inequality constraints of the form
 ,
where the functions
,
where the functions
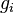 are convex
are convex - Equality constraints of the form
 ,
where the functions
,
where the functions
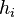 are preserved linearly after the transformation. In practice, the terms "linear"
and "affine" are often used interchangeably. Such constraints can be expressed
in the form
are preserved linearly after the transformation. In practice, the terms "linear"
and "affine" are often used interchangeably. Such constraints can be expressed
in the form
 ,
where
,
where
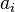 is a column-vector and
is a column-vector and
 a real number.
a real number.
A convex minimization case is thus written as
Note that every equality constraint
 can be equivalently replaced by a pair of inequality constraints
can be equivalently replaced by a pair of inequality constraints
 and
and
 .
.
Following from this fact, it is easy to understand why
 has to be affine(preserved linearly) as opposed to merely being convex. If
has to be affine(preserved linearly) as opposed to merely being convex. If
 is convex,
is convex,
 is convex, but
is convex, but
 is concave. Therefore, the only way for
is concave. Therefore, the only way for
 to be convex is for
to be convex is for
 to be affine.
to be affine.
Lagrange multipliers
Consider a convex minimization problem given in standard form by a cost function
 and inequality constraints
and inequality constraints
 ,
where
,
where
 .
Then the domain
.
Then the domain
 is:
is:
The Lagrangian function for the problem is
- L(x,λ0,...,λm) = λ0f(x) + λ1g1(x) + ... + λmgm(x).
For each point x in X that minimizes f over X, there exist real numbers λ0, ..., λm, called Lagrange multipliers, that satisfy these conditions simultaneously:
- x minimizes L(y, λ0, λ1, ..., λm) over all y in X,
- λ0 ≥ 0, λ1 ≥ 0, ..., λm ≥ 0, with at least one λk>0,
- λ1g1(x) = 0, ..., λmgm(x) = 0 (complementary slackness).
If there exists a "strictly feasible point", i.e., a point z satisfying
- g1(z) < 0,...,gm(z) < 0,
then the statement above can be upgraded to assert that λ0=1.
Conversely, if some x in X satisfies 1-3 for scalars λ0, ..., λm with λ0 = 1, then x is certain to minimize f over X.
Notes
- ^ Hiriart-Urruty, Jean-Baptiste; Lemaréchal, Claude (1996). Convex analysis and minimization algorithms: Fundamentals. p. 291. http://books.google.de/books?id=Gdl4Jc3RVjcC&printsec=frontcover&dq=lemarechal+convex+analysis+and+minimization&hl=de&sa=X&ei=E602T4GXGMzQsgaPtJ2VDA&ved=0CDUQ6AEwAA#v=onepage&q=convex%20minimization&f=false.
- ^ Ben-Tal, Aharon; Nemirovskiĭ, Arkadiĭ Semenovich (2001). Lectures on modern convex optimization: analysis, algorithms, and engineering applications. pp. 335–336. http://books.google.de/books?id=M3MqpEJ3jzQC&printsec=frontcover&dq=Lectures+on+Modern+Convex+Optimization:+Analysis,+Algorithms,&hl=de&sa=X&ei=26c2T6G7HYrIswac0d2uDA&ved=0CDIQ6AEwAA#v=onepage&q=convex%20programming&f=false.
- ^ Boyd/Vandenberghe, p. 7
- ^ For methods for convex minimization, see the volumes by Hiriart-Urruty and Lemaréchal (bundle) and the textbooks by Ruszczynski and Boyd and Vandenberghe (interior point).
- ^ Bertsekas
- ^ Hiriart-Urruty & Lemaréchal (1993, Example XV.1.1.2, p. 277) discuss a "bad guy" constructed by Arkadi Nemirovskii.
- ^
In theory, quasiconvex programming and
convex programming problems can be solved in reasonable amount of time, where
the number of iterations grows like a polynomial in the dimension of the problem
(and in the reciprocal of the approximation error tolerated):
Kiwiel, Krzysztof C. (2001). "Convergence and efficiency of subgradient methods for quasiconvex minimization". Mathematical Programming (Series A) (Berlin, Heidelberg: Springer) 90 (1): pp. 1–25. doi:10.1007/PL00011414. ISSN 0025-5610. MR 1819784.Kiwiel acknowledges that Yuri Nesterov first established that quasiconvex minimization problems can be solved efficiently.
- ^ Nemirovskii and Judin
- ^ Convex maximization is mentioned in the subsection on convex optimization in this textbook: Ulrich Faigle, Walter Kern, and George Still. Algorithmic principles of mathematical programming. Springer-Verlag. Texts in Mathematics. Chapter 10.2, Subsection "Convex optimization", pages 205-206.
- ^ Theorem 32.1 in Rockafellar's Convex Analysis states this maximum principle for extended real-valued functions.
- ^ Sahni, S. "Computationally related problems," in SIAM Journal on Computing, 3, 262--279, 1974.
- ^ Quadratic programming with one negative eigenvalue is NP-hard, Panos M. Pardalos and Stephen A. Vavasis in Journal of Global Optimization, Volume 1, Number 1, 1991, pg.15-22.
Xgains4keeps Inc




